圖的廣度優(yōu)先遍歷即橫向優(yōu)先遍歷,類似于二叉樹的按層遍歷。廣度優(yōu)先遍歷是從根結(jié)點(diǎn)開始沿著樹的寬度搜索遍歷,即按層次的去遍歷;從上往下對每一層依次訪問,在每層中,從左往右(或右往左)訪問結(jié)點(diǎn),訪問完一層就進(jìn)入下一層,直到?jīng)]有結(jié)點(diǎn)可以訪問為止。

1.前言
和樹的遍歷類似,圖的遍歷也是從圖中某點(diǎn)出發(fā),然后按照某種方法對圖中所有頂點(diǎn)進(jìn)行訪問,且僅訪問一次。
但是圖的遍歷相對樹而言要更為復(fù)雜。因?yàn)閳D中的任意頂點(diǎn)都可能與其他頂點(diǎn)相鄰,所以在圖的遍歷中必須記錄已被訪問的頂點(diǎn),避免重復(fù)訪問。
根據(jù)搜索路徑的不同,我們可以將遍歷圖的方法分為兩種:廣度優(yōu)先搜索和深度優(yōu)先搜索。
2.圖的基本概念
2.1.無向圖和無向圖
頂點(diǎn)對(u,v)是無序的,即(u,v)和(v,u)是同一條邊。常用一對圓括號表示。
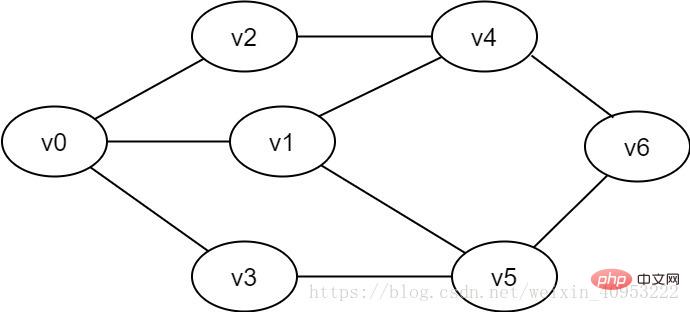
圖2-1-1 無向圖示例
頂點(diǎn)對<u,v>是有序的,它是指從頂點(diǎn)u到頂點(diǎn) v的一條有向邊。其中u是有向邊的始點(diǎn),v是有向邊的終點(diǎn)。常用一對尖括號表示。
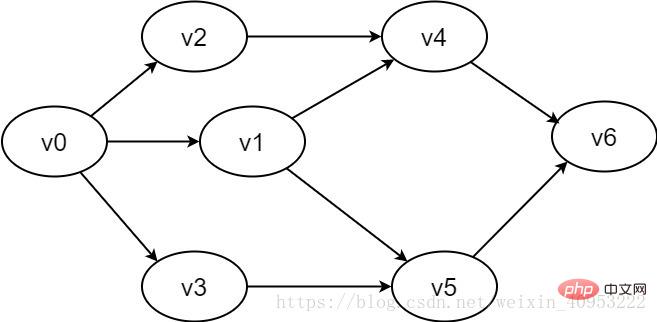
圖2-1-2 有向圖示例
2.2.權(quán)和網(wǎng)
圖的每條邊上可能存在具有某種含義的數(shù)值,稱該數(shù)值為該邊上的權(quán)。而這種帶權(quán)的圖被稱為網(wǎng)。
2.3.連通圖與非連通圖
連通圖:在無向圖G中,從頂點(diǎn)v到頂點(diǎn)v'有路徑,則稱v和v'是聯(lián)通的。若圖中任意兩頂點(diǎn)v、v'∈V,v和v'之間均聯(lián)通,則稱G是連通圖。上述兩圖均為連通圖。
非連通圖:若無向圖G中,存在v和v'之間不連通,則稱G是非連通圖。
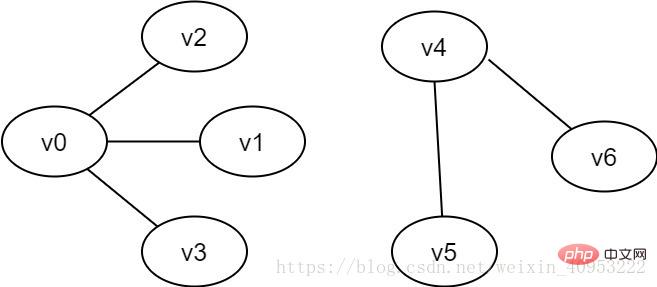
圖2-3 非連通圖示例
3.廣度優(yōu)先搜索
3.1.算法的基本思路
廣度優(yōu)先搜索類似于樹的層次遍歷過程。它需要借助一個隊列來實(shí)現(xiàn)。如圖2-1-1所示,要想遍歷從v0到v6的每一個頂點(diǎn),我們可以設(shè)v0為第一層,v1、v2、v3為第二層,v4、v5為第三層,v6為第四層,再逐個遍歷每一層的每個頂點(diǎn)。
具體過程如下:
1.準(zhǔn)備工作:創(chuàng)建一個visited數(shù)組,用來記錄已被訪問過的頂點(diǎn);創(chuàng)建一個隊列,用來存放每一層的頂點(diǎn);初始化圖G。
2.從圖中的v0開始訪問,將的visited[v0]數(shù)組的值設(shè)置為true,同時將v0入隊。
3.只要隊列不空,則重復(fù)如下操作:
(1)隊頭頂點(diǎn)u出隊。
(2)依次檢查u的所有鄰接頂點(diǎn)w,若visited[w]的值為false,則訪問w,并將visited[w]置為true,同時將w入隊。
3.2.算法的實(shí)現(xiàn)過程
白色表示未被訪問,灰色表示即將訪問,黑色表示已訪問。
visited數(shù)組:0表示未訪問,1表示以訪問。
隊列:隊頭出元素,隊尾進(jìn)元素。
1.初始時全部頂點(diǎn)均未被訪問,visited數(shù)組初始化為0,隊列中沒有元素。
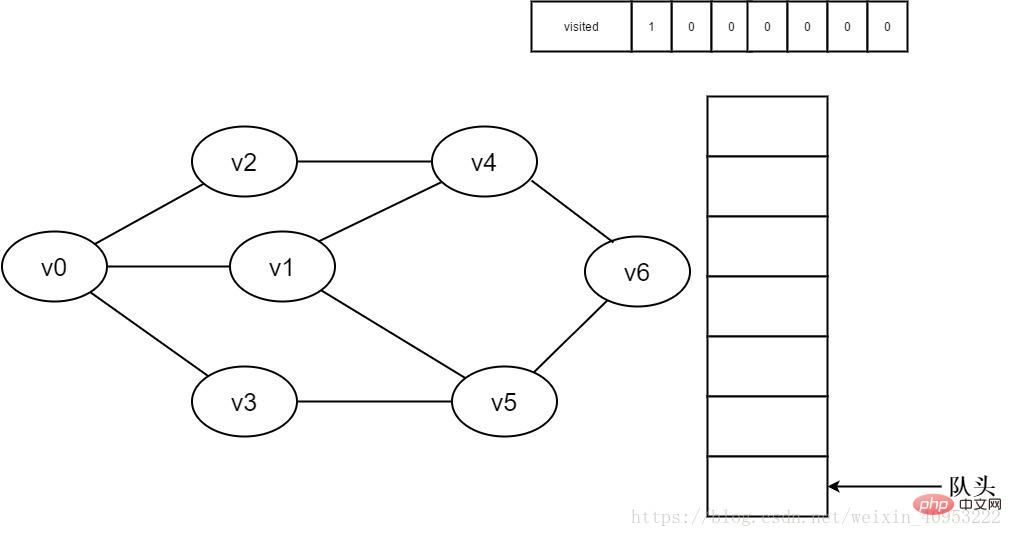
圖3-2-1
2.即將訪問頂點(diǎn)v0。
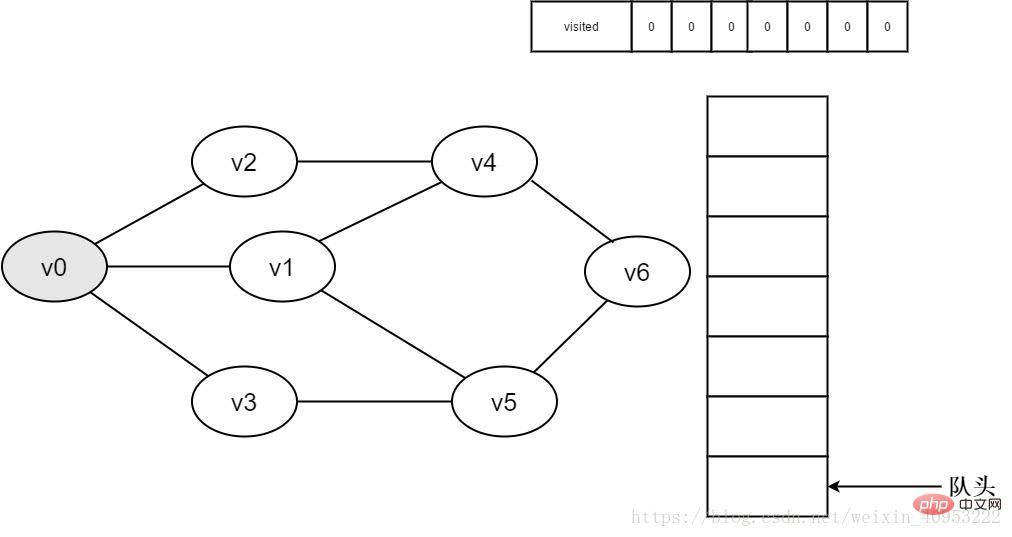
圖3-2-2
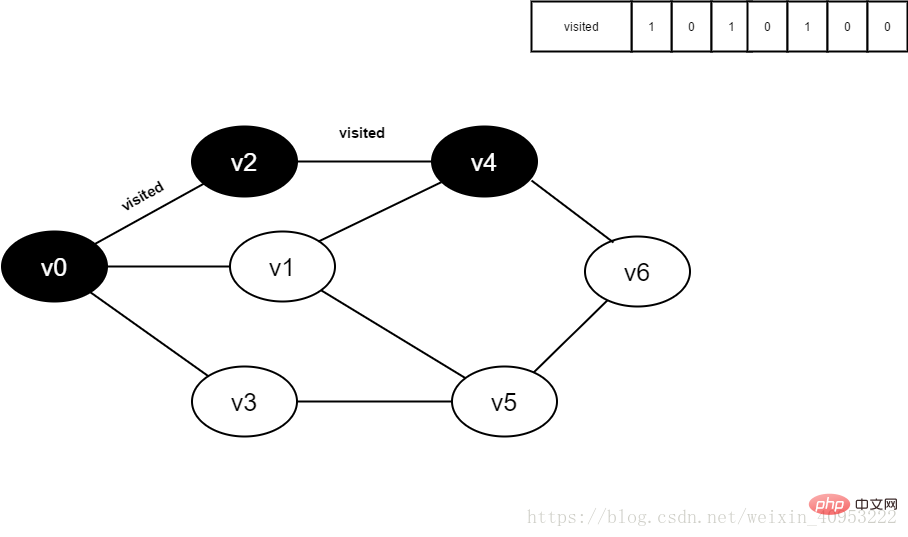
3.訪問頂點(diǎn)v0,并置visited[0]的值為1,同時將v0入隊。
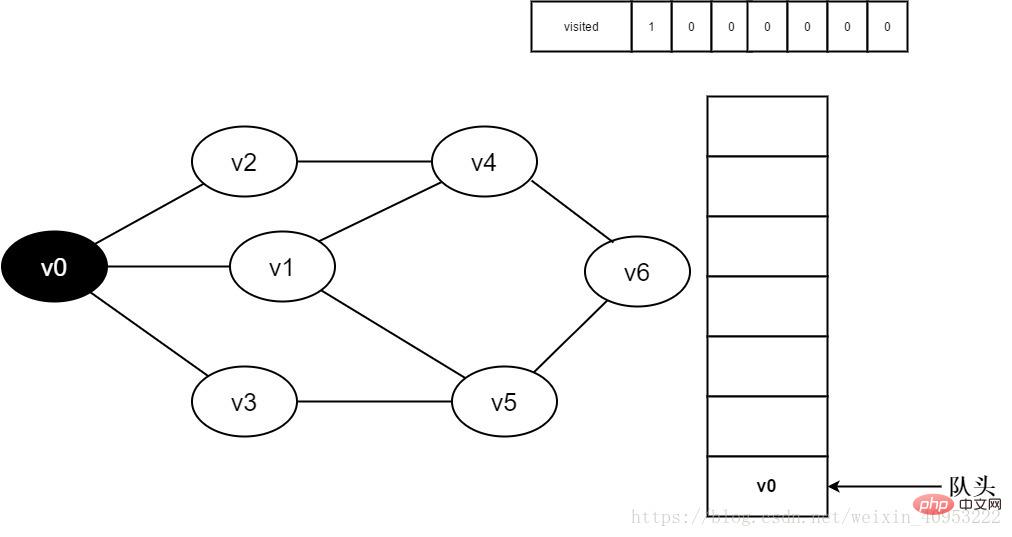
圖3-2-3
4.將v0出隊,訪問v0的鄰接點(diǎn)v2。判斷visited[2],因?yàn)関isited[2]的值為0,訪問v2。
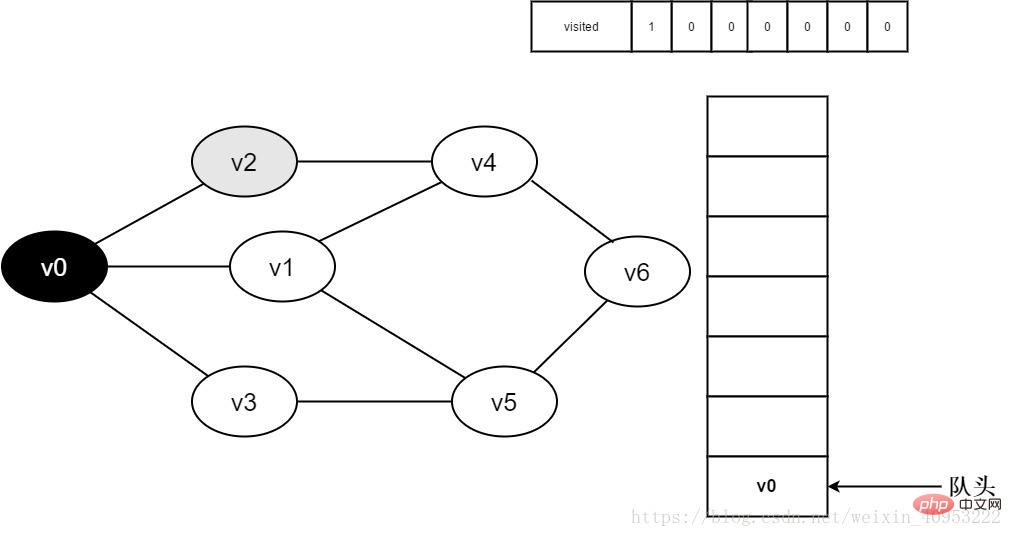
圖3-2-4
5.將visited[2]置為1,并將v2入隊。
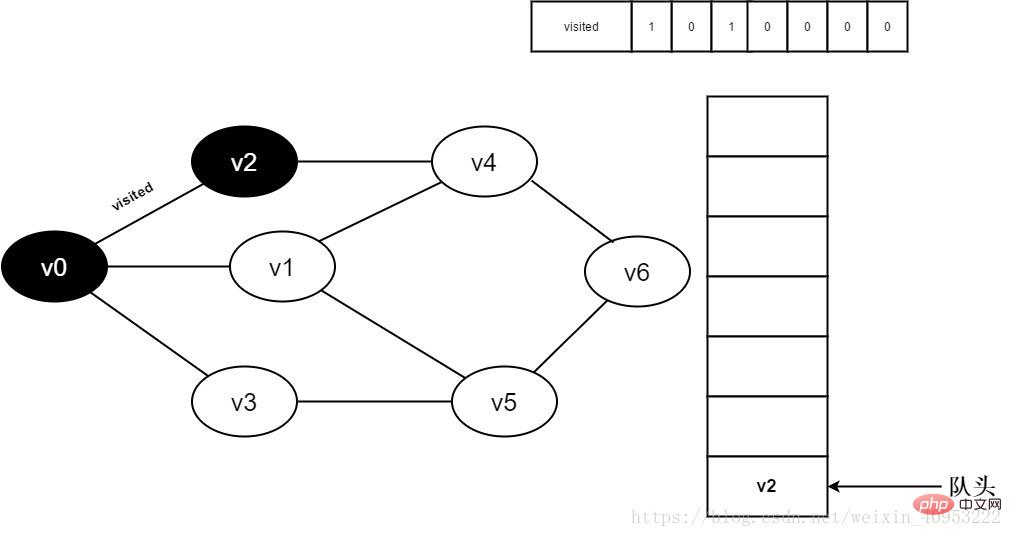
圖3-2-5
6.訪問v0鄰接點(diǎn)v1。判斷visited[1],因?yàn)関isited[1]的值為0,訪問v1。
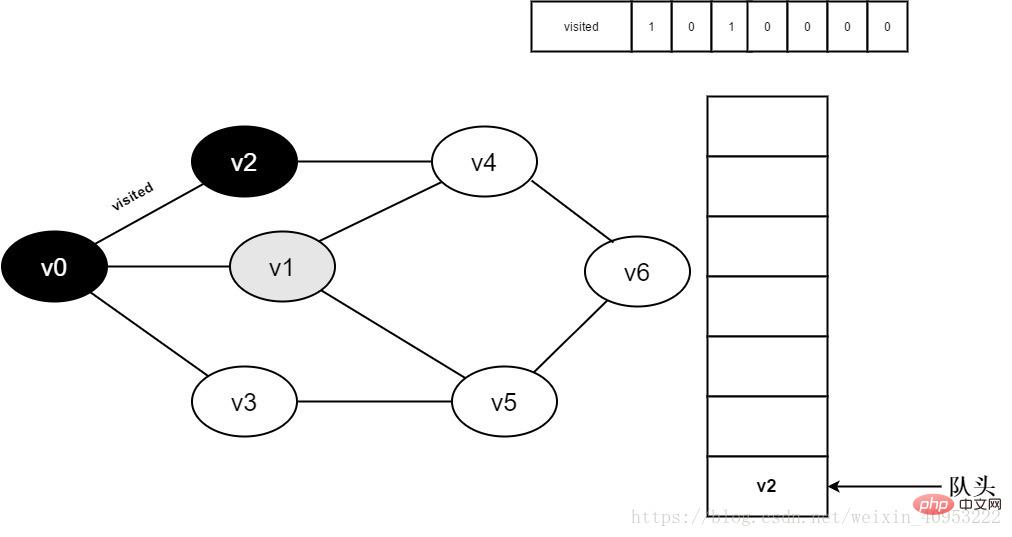
圖3-2-6
7.將visited[1]置為0,并將v1入隊。
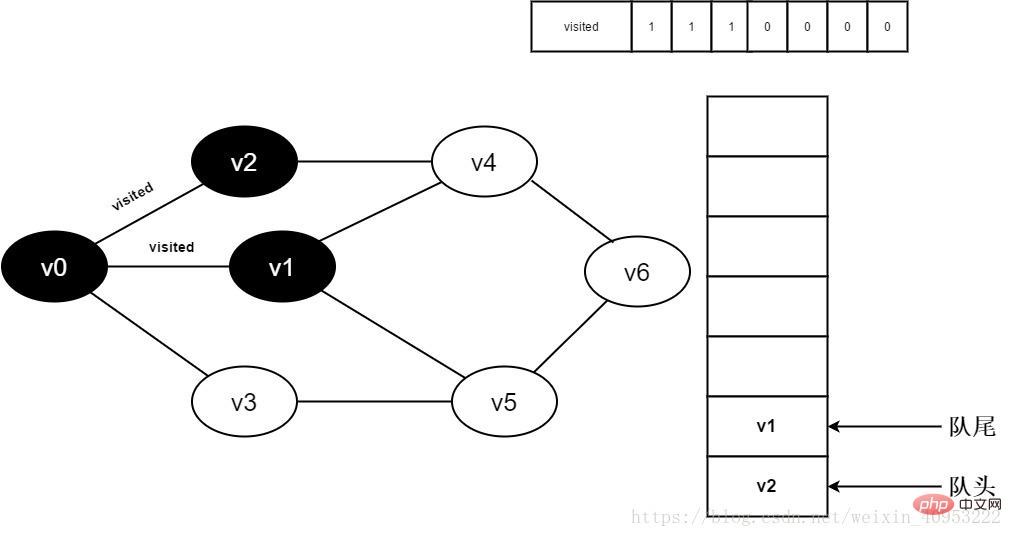
圖3-2-7
8.判斷visited[3],因?yàn)樗闹禐?,訪問v3。將visited[3]置為0,并將v3入隊。
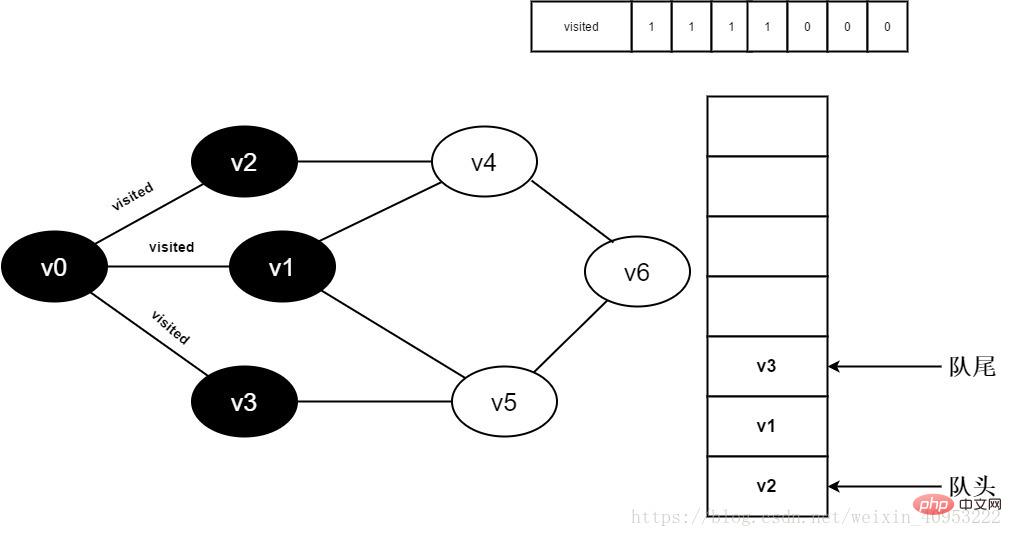
圖3-2-8
9.v0的全部鄰接點(diǎn)均已被訪問完畢。將隊頭元素v2出隊,開始訪問v2的所有鄰接點(diǎn)。
開始訪問v2鄰接點(diǎn)v0,判斷visited[0],因?yàn)槠渲禐?,不進(jìn)行訪問。
繼續(xù)訪問v2鄰接點(diǎn)v4,判斷visited[4],因?yàn)槠渲禐?,訪問v4,如下圖:
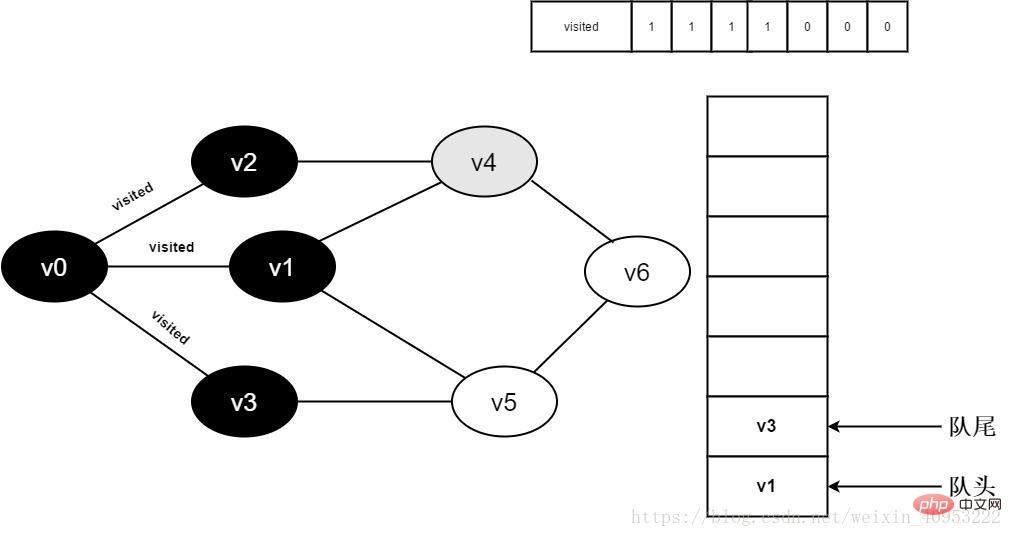
圖3-2-9
10.將visited[4]置為1,并將v4入隊。

圖3-2-10
11.v2的全部鄰接點(diǎn)均已被訪問完畢。將隊頭元素v1出隊,開始訪問v1的所有鄰接點(diǎn)。
開始訪問v1鄰接點(diǎn)v0,因?yàn)関isited[0]值為1,不進(jìn)行訪問。
繼續(xù)訪問v1鄰接點(diǎn)v4,因?yàn)関isited[4]的值為1,不進(jìn)行訪問。
繼續(xù)訪問v1鄰接點(diǎn)v5,因?yàn)関isited[5]值為0,訪問v5,如下圖:

圖3-2-11
12.將visited[5]置為1,并將v5入隊。
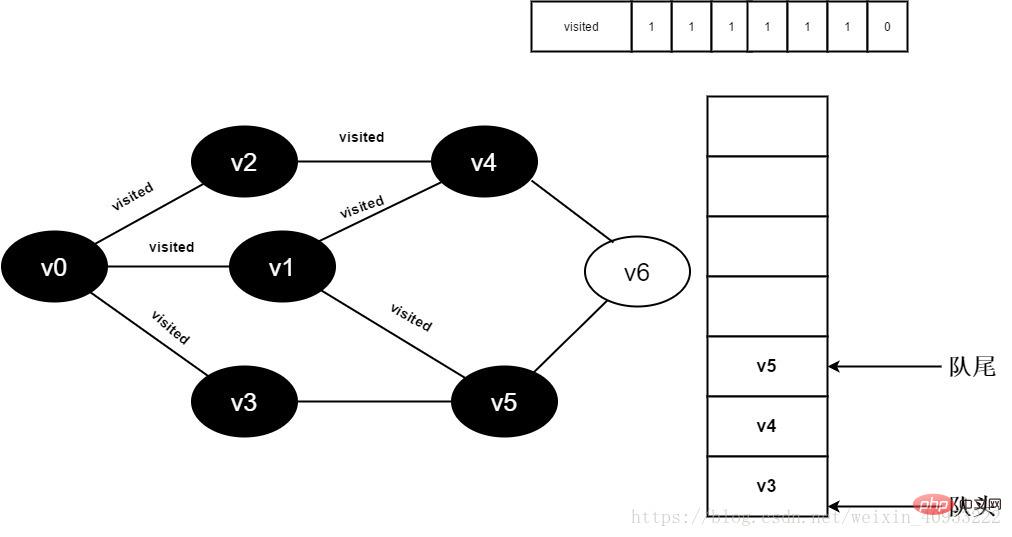
圖3-2-12
13.v1的全部鄰接點(diǎn)均已被訪問完畢,將隊頭元素v3出隊,開始訪問v3的所有鄰接點(diǎn)。
開始訪問v3鄰接點(diǎn)v0,因?yàn)関isited[0]值為1,不進(jìn)行訪問。
繼續(xù)訪問v3鄰接點(diǎn)v5,因?yàn)関isited[5]值為1,不進(jìn)行訪問。
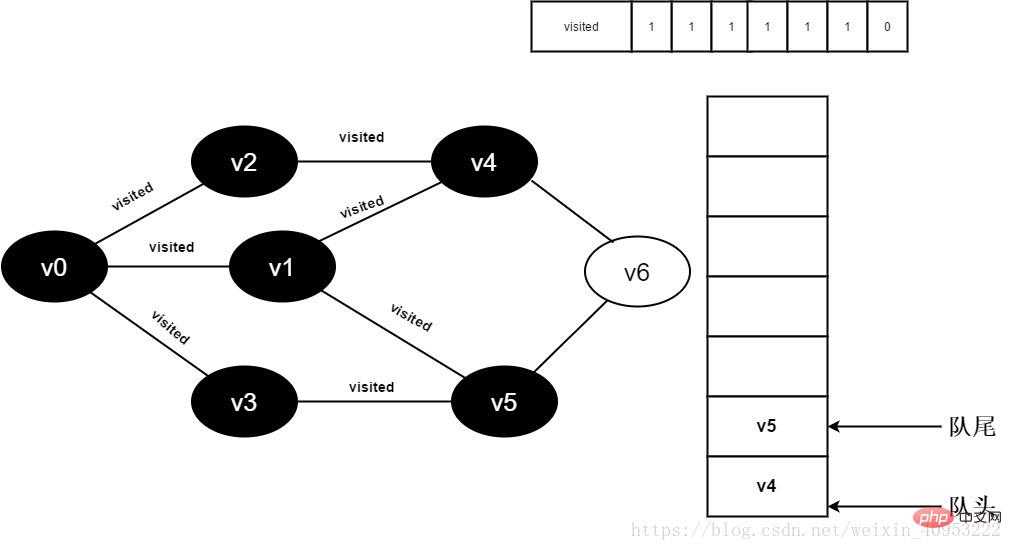
圖3-2-13
14.v3的全部鄰接點(diǎn)均已被訪問完畢,將隊頭元素v4出隊,開始訪問v4的所有鄰接點(diǎn)。
開始訪問v4的鄰接點(diǎn)v2,因?yàn)関isited[2]的值為1,不進(jìn)行訪問。
繼續(xù)訪問v4的鄰接點(diǎn)v6,因?yàn)関isited[6]的值為0,訪問v6,如下圖:
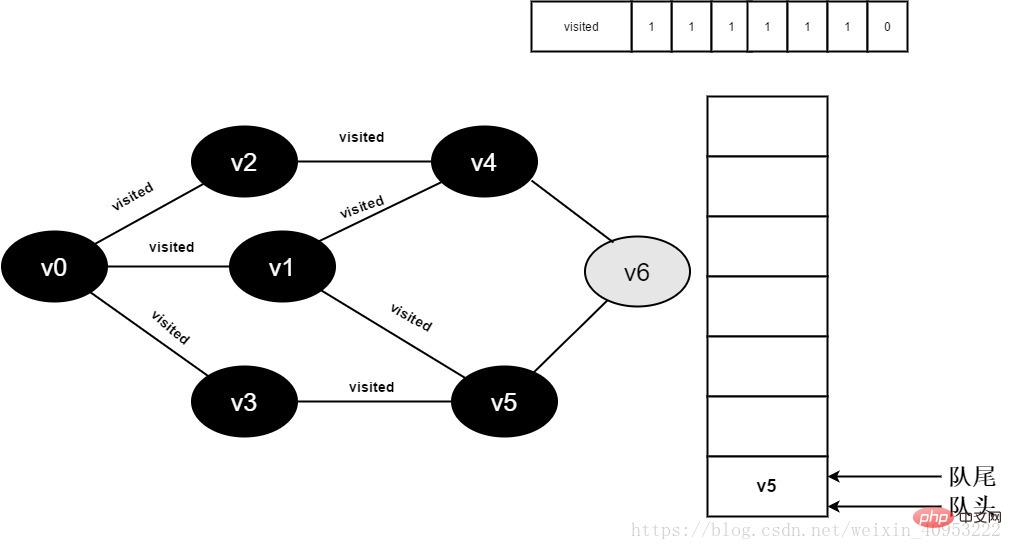
圖3-2-14
15.將visited[6]值為1,并將v6入隊。
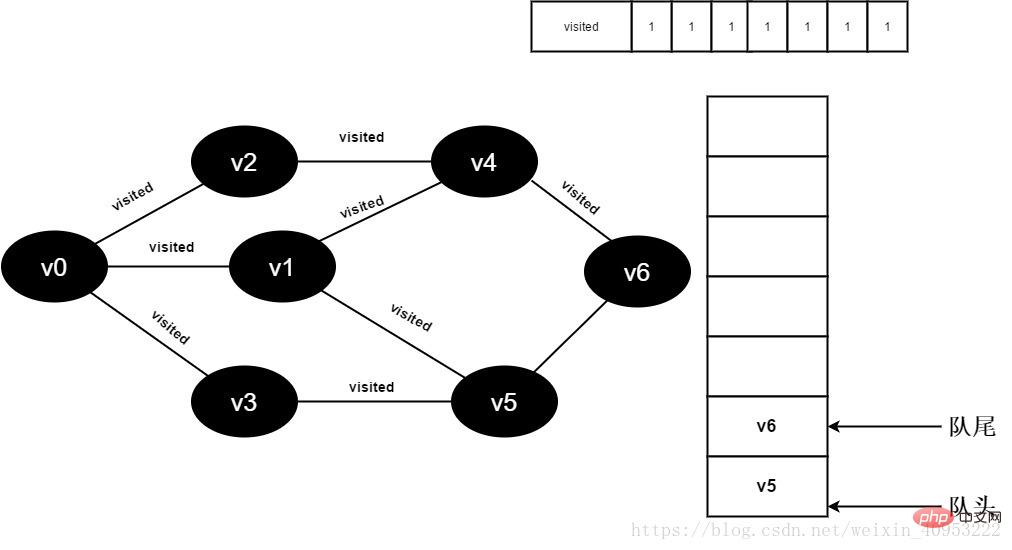
圖3-2-15
16.v4的全部鄰接點(diǎn)均已被訪問完畢,將隊頭元素v5出隊,開始訪問v5的所有鄰接點(diǎn)。
開始訪問v5鄰接點(diǎn)v3,因?yàn)関isited[3]的值為1,不進(jìn)行訪問。
繼續(xù)訪問v5鄰接點(diǎn)v6,因?yàn)関isited[6]的值為1,不進(jìn)行訪問。
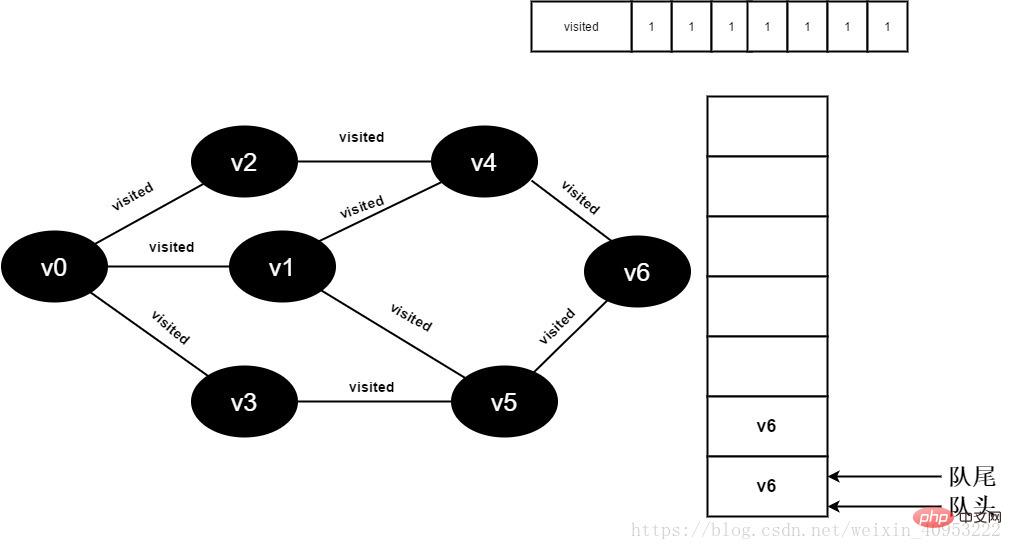
圖3-2-16
17.v5的全部鄰接點(diǎn)均已被訪問完畢,將隊頭元素v6出隊,開始訪問v6的所有鄰接點(diǎn)。
開始訪問v6鄰接點(diǎn)v4,因?yàn)関isited[4]的值為1,不進(jìn)行訪問。
繼續(xù)訪問v6鄰接點(diǎn)v5,因?yàn)関isited[5]的值文1,不進(jìn)行訪問。
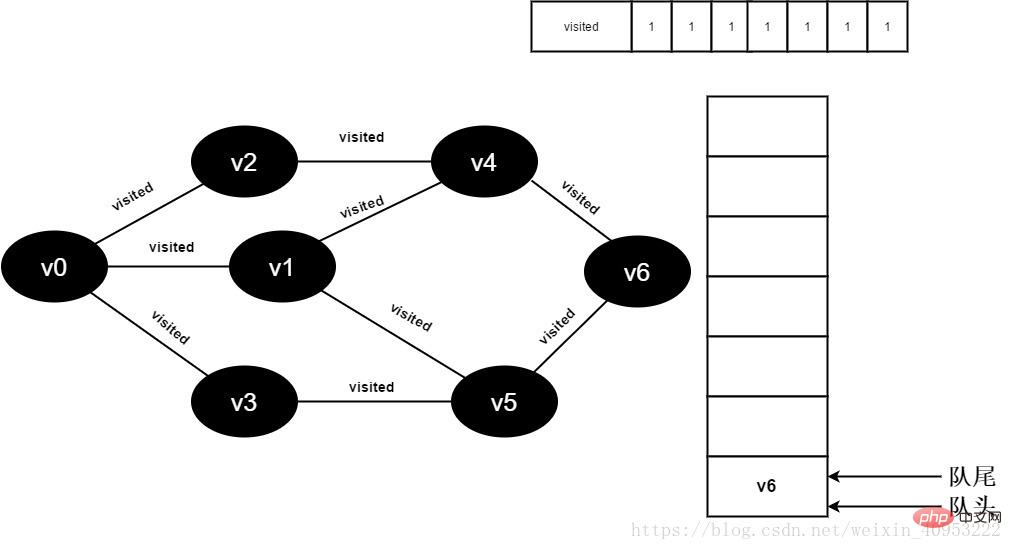
圖3-2-17
18.隊列為空,退出循環(huán),全部頂點(diǎn)均訪問完畢。

圖3-2-18
3.3具體代碼的實(shí)現(xiàn)
3.3.1用鄰接矩陣表示圖的廣度優(yōu)先搜索
/*一些量的定義*/ queue<char> q; //定義一個隊列,使用庫函數(shù)queue #define MVNum 100 //表示最大頂點(diǎn)個數(shù) bool visited[MVNum]; //定義一個visited數(shù)組,記錄已被訪問的頂點(diǎn)
/*鄰接矩陣存儲表示*/ typedef struct AMGraph { char vexs[MVNum]; //頂點(diǎn)表 int arcs[MVNum][MVNum]; //鄰接矩陣 int vexnum, arcnum; //當(dāng)前的頂點(diǎn)數(shù)和邊數(shù) } AMGraph;
/*找到頂點(diǎn)v的對應(yīng)下標(biāo)*/ int LocateVex(AMGraph &G, char v) { int i; for (i = 0; i < G.vexnum; i++) if (G.vexs[i] == v) return i; }
/*采用鄰接矩陣表示法,創(chuàng)建無向圖G*/ int CreateUDG_1(AMGraph &G) { int i, j, k; char v1, v2; scanf("%d%d", &G.vexnum, &G.arcnum); //輸入總頂點(diǎn)數(shù),總邊數(shù) getchar(); //獲取'n’,防止其對之后的字符輸入造成影響 for (i = 0; i < G.vexnum; i++) scanf("%c", &G.vexs[i]); //依次輸入點(diǎn)的信息 for (i = 0; i < G.vexnum; i++) for (j = 0; j < G.vexnum; j++) G.arcs[i][j] = 0; //初始化鄰接矩陣邊,0表示頂點(diǎn)i和j之間無邊 for (k = 0; k < G.arcnum; k++) { getchar(); scanf("%c%c", &v1, &v2); //輸入一條邊依附的頂點(diǎn) i = LocateVex(G, v1); //找到頂點(diǎn)i的下標(biāo) j = LocateVex(G, v2); //找到頂點(diǎn)j的下標(biāo) G.arcs[i][j] = G.arcs[j][i] = 1; //1表示頂點(diǎn)i和j之間有邊,無向圖不區(qū)分方向 } return 1; }
/*采用鄰接矩陣表示圖的廣度優(yōu)先遍歷*/ void BFS_AM(AMGraph &G,char v0) { /*從v0元素開始訪問圖*/ int u,i,v,w; v = LocateVex(G,v0); //找到v0對應(yīng)的下標(biāo) printf("%c ", v0); //打印v0 visited[v] = 1; //頂點(diǎn)v0已被訪問 q.push(v0); //將v0入隊 while (!q.empty()) { u = q.front(); //將隊頭元素u出隊,開始訪問u的所有鄰接點(diǎn) v = LocateVex(G, u); //得到頂點(diǎn)u的對應(yīng)下標(biāo) q.pop(); //將頂點(diǎn)u出隊 for (i = 0; i < G.vexnum; i++) { w = G.vexs[i]; if (G.arcs[v][i] && !visited[i])//頂點(diǎn)u和w間有邊,且頂點(diǎn)w未被訪問 { printf("%c ", w); //打印頂點(diǎn)w q.push(w); //將頂點(diǎn)w入隊 visited[i] = 1; //頂點(diǎn)w已被訪問 } } } }
3.3.2用鄰接表表示圖的廣度優(yōu)先搜索
/*找到頂點(diǎn)對應(yīng)的下標(biāo)*/ int LocateVex(ALGraph &G, char v) { int i; for (i = 0; i < G.vexnum; i++) if (v == G.vertices[i].data) return i; }
/*鄰接表存儲表示*/ typedef struct ArcNode //邊結(jié)點(diǎn) { int adjvex; //該邊所指向的頂點(diǎn)的位置 ArcNode *nextarc; //指向下一條邊的指針 int info; //和邊相關(guān)的信息,如權(quán)值 }ArcNode; typedef struct VexNode //表頭結(jié)點(diǎn) { char data; ArcNode *firstarc; //指向第一條依附該頂點(diǎn)的邊的指針 }VexNode,AdjList[MVNum]; //AbjList表示一個表頭結(jié)點(diǎn)表 typedef struct ALGraph { AdjList vertices; int vexnum, arcnum; }ALGraph;
/*采用鄰接表表示法,創(chuàng)建無向圖G*/ int CreateUDG_2(ALGraph &G) { int i, j, k; char v1, v2; scanf("%d%d", &G.vexnum, &G.arcnum); //輸入總頂點(diǎn)數(shù),總邊數(shù) getchar(); for (i = 0; i < G.vexnum; i++) //輸入各頂點(diǎn),構(gòu)造表頭結(jié)點(diǎn)表 { scanf("%c", &G.vertices[i].data); //輸入頂點(diǎn)值 G.vertices[i].firstarc = NULL; //初始化每個表頭結(jié)點(diǎn)的指針域?yàn)镹ULL } for (k = 0; k < G.arcnum; k++) //輸入各邊,構(gòu)造鄰接表 { getchar(); scanf("%c%c", &v1, &v2); //輸入一條邊依附的兩個頂點(diǎn) i = LocateVex(G, v1); //找到頂點(diǎn)i的下標(biāo) j = LocateVex(G, v2); //找到頂點(diǎn)j的下標(biāo) ArcNode *p1 = new ArcNode; //創(chuàng)建一個邊結(jié)點(diǎn)*p1 p1->adjvex = j; //其鄰接點(diǎn)域?yàn)閖 p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p1; // 將新結(jié)點(diǎn)*p插入到頂點(diǎn)v1的邊表頭部 ArcNode *p2 = new ArcNode; //生成另一個對稱的新的表結(jié)點(diǎn)*p2 p2->adjvex = i; p2->nextarc = G.vertices[j].firstarc; G.vertices[j].firstarc = p1; } return 1; }
/*采用鄰接表表示圖的廣度優(yōu)先遍歷*/ void BFS_AL(ALGraph &G, char v0) { int u,w,v; ArcNode *p; printf("%c ", v0); //打印頂點(diǎn)v0 v = LocateVex(G, v0); //找到v0對應(yīng)的下標(biāo) visited[v] = 1; //頂點(diǎn)v0已被訪問 q.push(v0); //將頂點(diǎn)v0入隊 while (!q.empty()) { u = q.front(); //將頂點(diǎn)元素u出隊,開始訪問u的所有鄰接點(diǎn) v = LocateVex(G, u); //得到頂點(diǎn)u的對應(yīng)下標(biāo) q.pop(); //將頂點(diǎn)u出隊 for (p = G.vertices[v].firstarc; p; p = p->nextarc) //遍歷頂點(diǎn)u的鄰接點(diǎn) { w = p->adjvex; if (!visited[w]) //頂點(diǎn)p未被訪問 { printf("%c ", G.vertices[w].data); //打印頂點(diǎn)p visited[w] = 1; //頂點(diǎn)p已被訪問 q.push(G.vertices[w].data); //將頂點(diǎn)p入隊 } } } }
3.4.非聯(lián)通圖的廣度優(yōu)先遍歷的實(shí)現(xiàn)方法
/*廣度優(yōu)先搜索非連通圖*/ void BFSTraverse(AMGraph G) { int v; for (v = 0; v < G.vexnum; v++) visited[v] = 0; //將visited數(shù)組初始化 for (v = 0; v < G.vexnum; v++) if (!visited[v]) BFS_AM(G, G.vexs[v]); //對尚未訪問的頂點(diǎn)調(diào)用BFS }
4.深度優(yōu)先搜索
4.1算法的基本思路
深度優(yōu)先搜索類似于樹的先序遍歷,具體過程如下:
準(zhǔn)備工作:創(chuàng)建一個visited數(shù)組,用于記錄所有被訪問過的頂點(diǎn)。
1.從圖中v0出發(fā),訪問v0。
2.找出v0的第一個未被訪問的鄰接點(diǎn),訪問該頂點(diǎn)。以該頂點(diǎn)為新頂點(diǎn),重復(fù)此步驟,直至剛訪問過的頂點(diǎn)沒有未被訪問的鄰接點(diǎn)為止。
3.返回前一個訪問過的仍有未被訪問鄰接點(diǎn)的頂點(diǎn),繼續(xù)訪問該頂點(diǎn)的下一個未被訪問領(lǐng)接點(diǎn)。
4.重復(fù)2,3步驟,直至所有頂點(diǎn)均被訪問,搜索結(jié)束。
4.2算法的實(shí)現(xiàn)過程
1.初始時所有頂點(diǎn)均未被訪問,visited數(shù)組為空。

圖4-2-1
2.即將訪問v0。

圖4-2-2
3.訪問v0,并將visited[0]的值置為1。
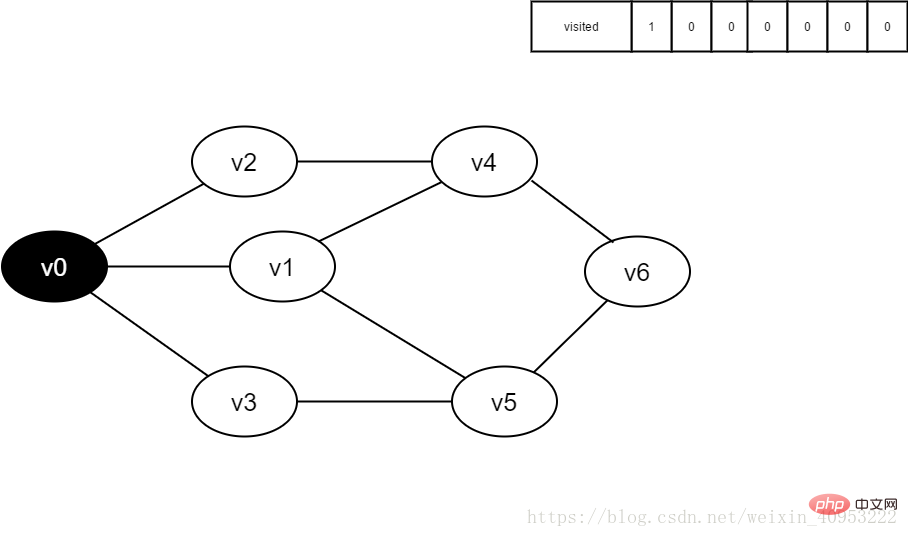
圖4-2-3
4.訪問v0的鄰接點(diǎn)v2,判斷visited[2],因其值為0,訪問v2。
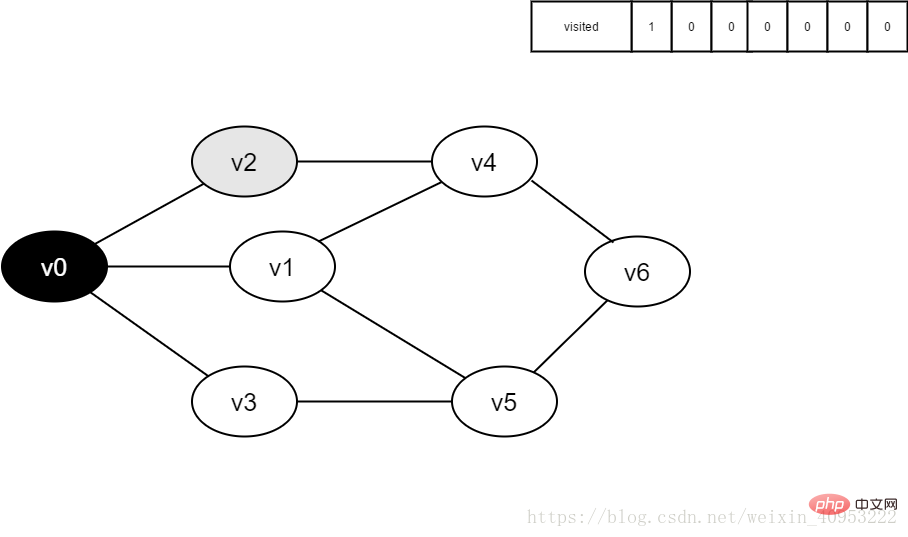
圖4-2-4
5.將visited[2]置為1。
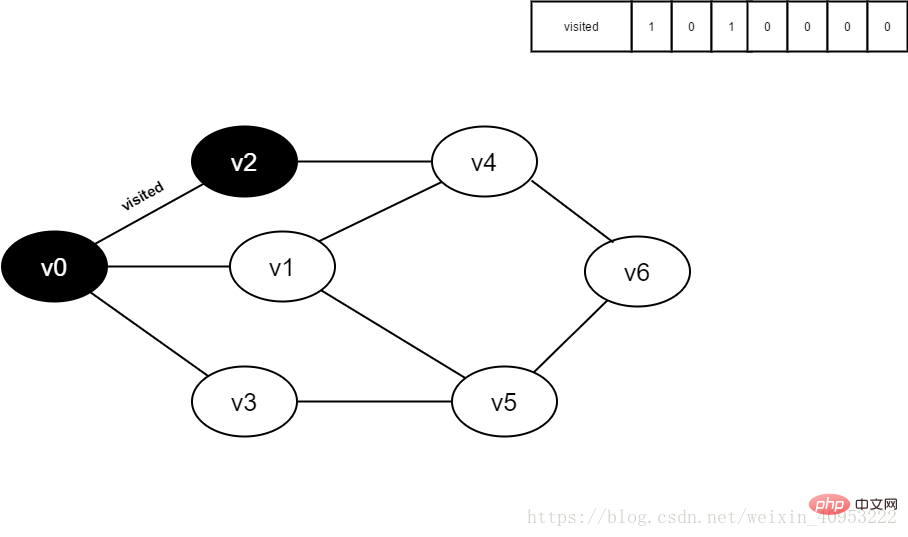
圖4-2-5
6.訪問v2的鄰接點(diǎn)v0,判斷visited[0],其值為1,不訪問。
繼續(xù)訪問v2的鄰接點(diǎn)v4,判斷visited[4],其值為0,訪問v4。
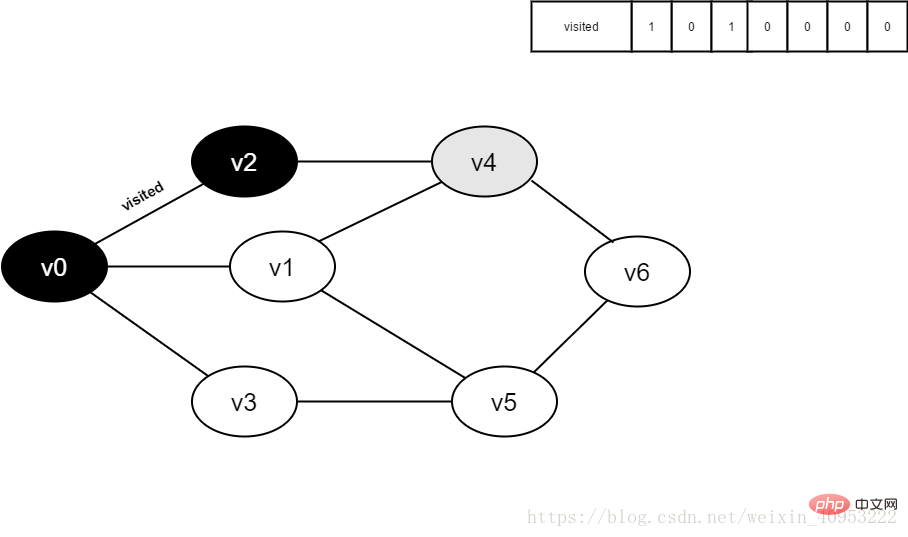
圖4-2-6
7.將visited[4]置為1。
圖4-2-7
8.訪問v4的鄰接點(diǎn)v1,判斷visited[1],其值為0,訪問v1。
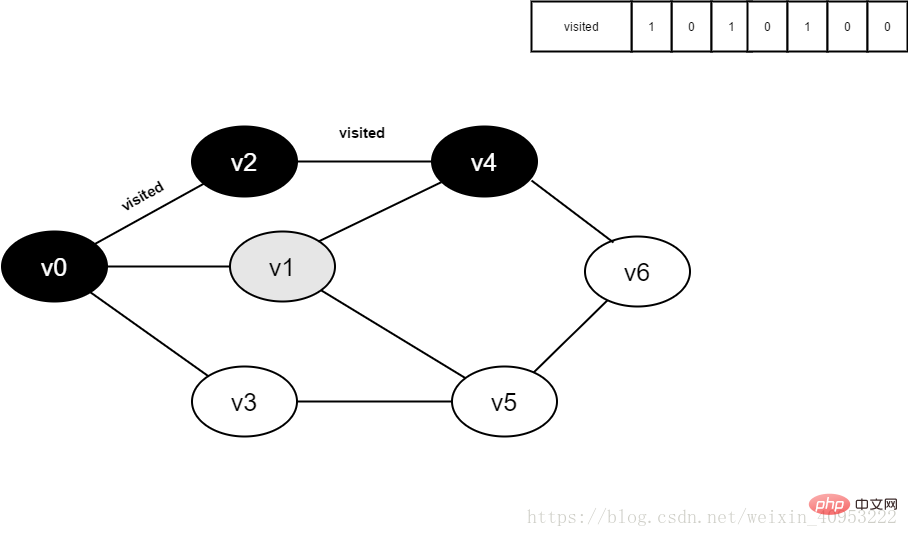
圖4-2-8
9.將visited[1]置為1。
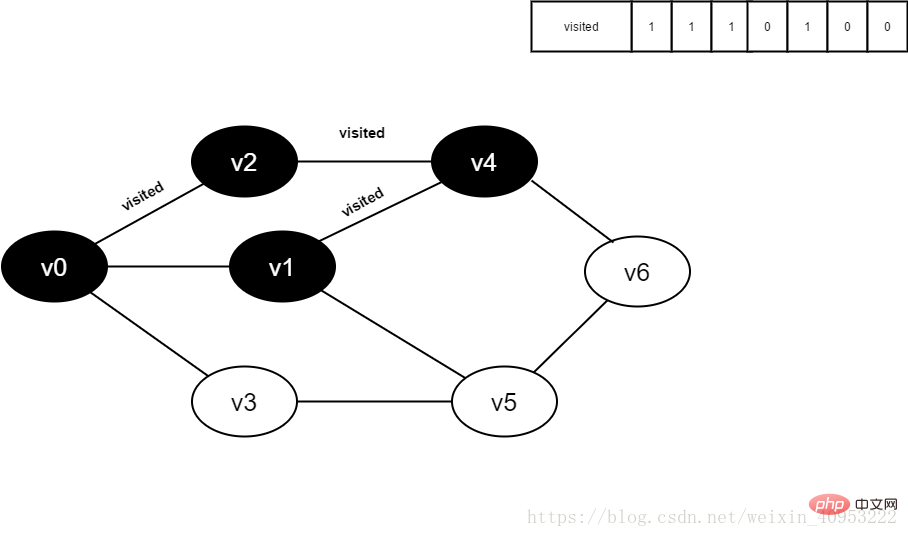
圖4-2-9
10.訪問v1的鄰接點(diǎn)v0,判斷visited[0],其值為1,不訪問。
繼續(xù)訪問v1的鄰接點(diǎn)v4,判斷visited[4],其值為1,不訪問。
繼續(xù)訪問v1的鄰接點(diǎn)v5,判讀visited[5],其值為0,訪問v5。
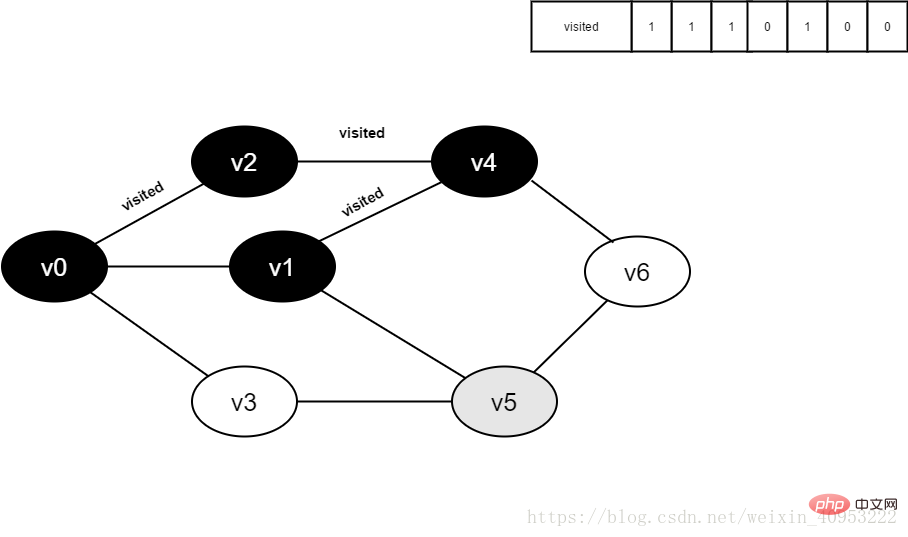
圖4-2-10
11.將visited[5]置為1。
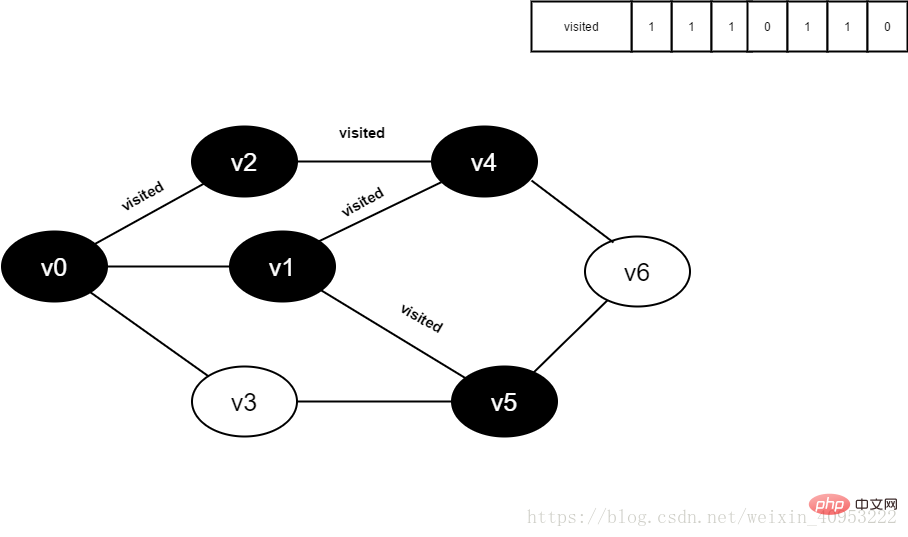
圖4-2-11
12.訪問v5的鄰接點(diǎn)v1,判斷visited[1],其值為1,不訪問。
繼續(xù)訪問v5的鄰接點(diǎn)v3,判斷visited[3],其值為0,訪問v3。
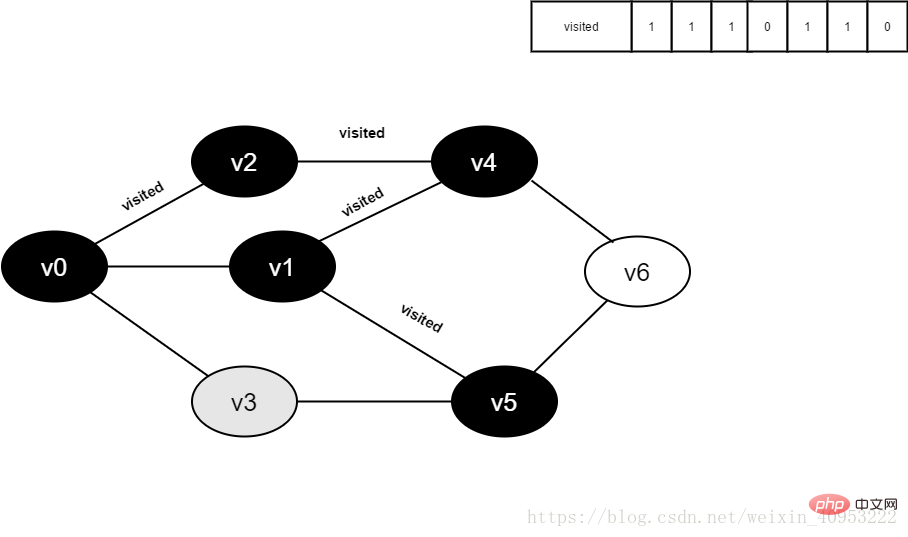
圖4-2-12
13.將visited[1]置為1。
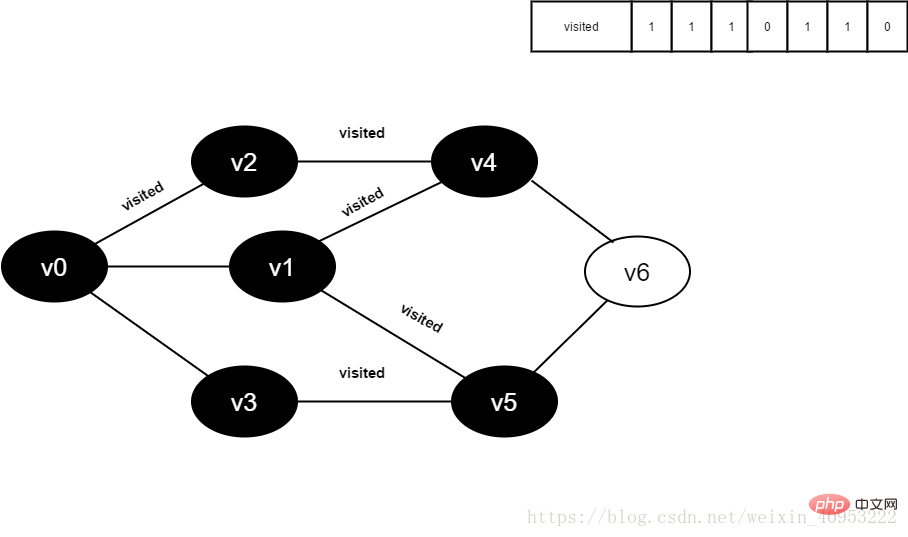
圖4-2-13
14.訪問v3的鄰接點(diǎn)v0,判斷visited[0],其值為1,不訪問。
繼續(xù)訪問v3的鄰接點(diǎn)v5,判斷visited[5],其值為1,不訪問。
v3所有鄰接點(diǎn)均已被訪問,回溯到其上一個頂點(diǎn)v5,遍歷v5所有鄰接點(diǎn)。
訪問v5的鄰接點(diǎn)v6,判斷visited[6],其值為0,訪問v6。
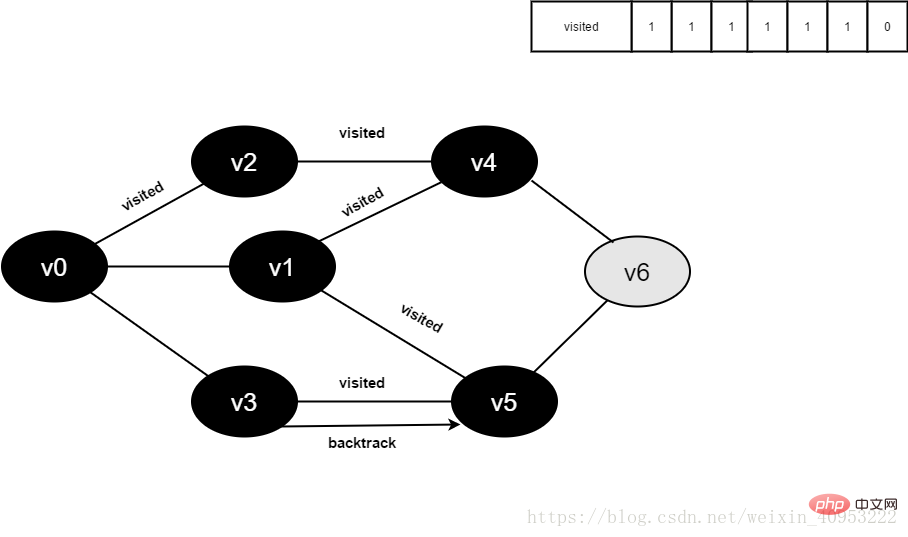
圖4-2-14
15.將visited[6]置為1。
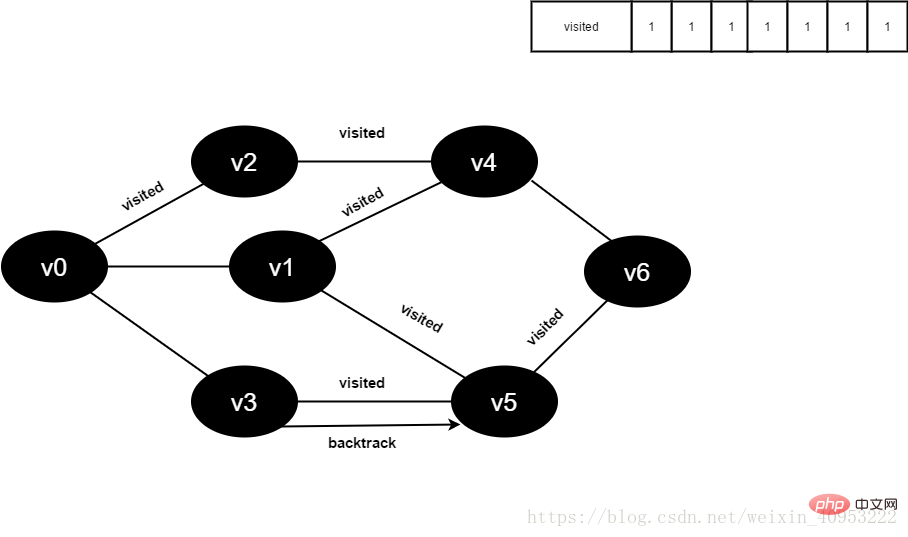
圖4-2-15
16.訪問v6的鄰接點(diǎn)v4,判斷visited[4],其值為1,不訪問。
訪問v6的鄰接點(diǎn)v5,判斷visited[5],其值為1,不訪問。
v6所有鄰接點(diǎn)均已被訪問,回溯到其上一個頂點(diǎn)v5,遍歷v5剩余鄰接點(diǎn)。
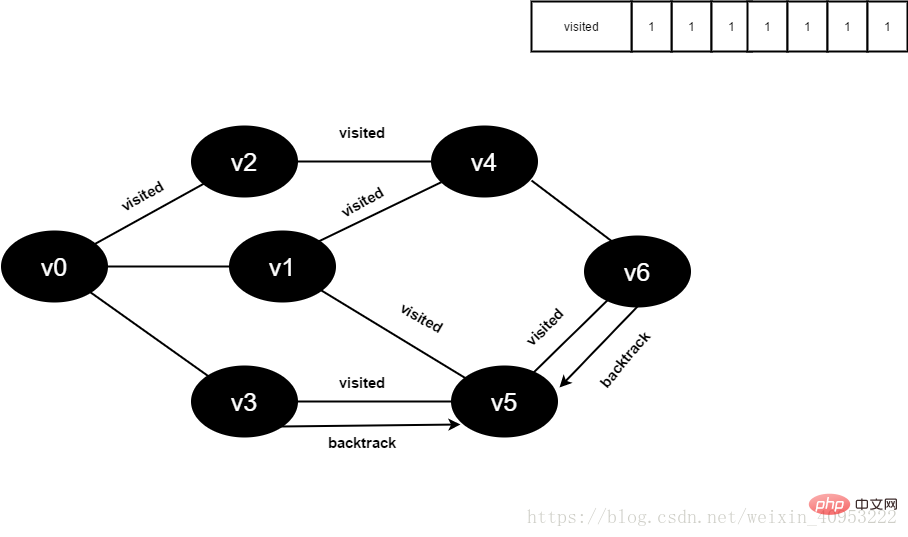
圖4-2-16
17.v5所有鄰接點(diǎn)均已被訪問,回溯到其上一個頂點(diǎn)v1。
v1所有鄰接點(diǎn)均已被訪問,回溯到其上一個頂點(diǎn)v4,遍歷v4剩余鄰接點(diǎn)v6。
v4所有鄰接點(diǎn)均已被訪問,回溯到其上一個頂點(diǎn)v2。
v2所有鄰接點(diǎn)均已被訪問,回溯到其上一個頂點(diǎn)v1,遍歷v1剩余鄰接點(diǎn)v3。
v1所有鄰接點(diǎn)均已被訪問,搜索結(jié)束。
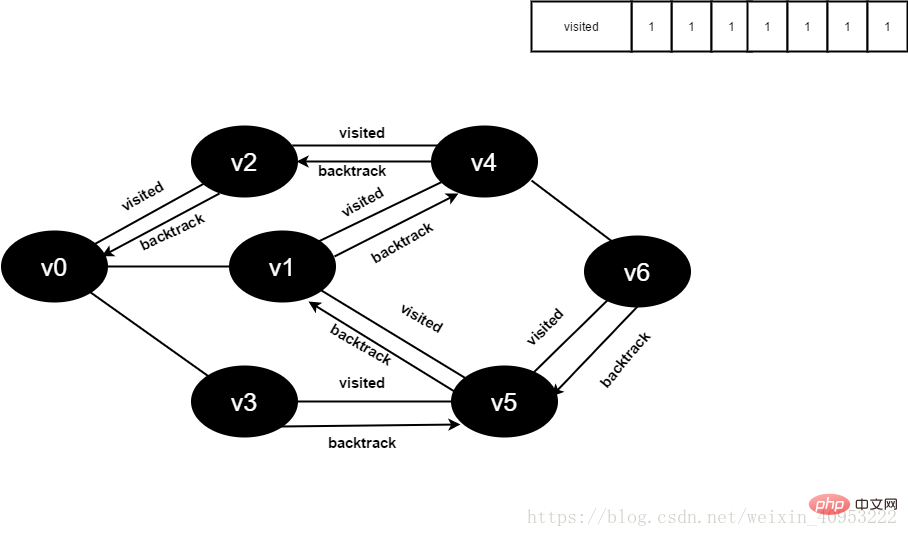
圖4-2-17
4.3具體代碼實(shí)現(xiàn)
4.3.1用鄰接矩陣表示圖的深度優(yōu)先搜索
鄰接矩陣的創(chuàng)建在上述已描述過,這里不再贅述
void DFS_AM(AMGraph &G, int v) { int w; printf("%c ", G.vexs[v]); visited[v] = 1; for (w = 0; w < G.vexnum; w++) if (G.arcs[v][w]&&!visited[w]) //遞歸調(diào)用 DFS_AM(G,w); }
4.3.2用鄰接表表示圖的深度優(yōu)先搜素
鄰接表的創(chuàng)建在上述已描述過,這里不再贅述。
void DFS_AL(ALGraph &G, int v) { int w; printf("%c ", G.vertices[v].data); visited[v] = 1; ArcNode *p = new ArcNode; p = G.vertices[v].firstarc; while (p) { w = p->adjvex; if (!visited[w]) DFS_AL(G, w); p = p->nextarc; } }
 站長資訊網(wǎng)
站長資訊網(wǎng)