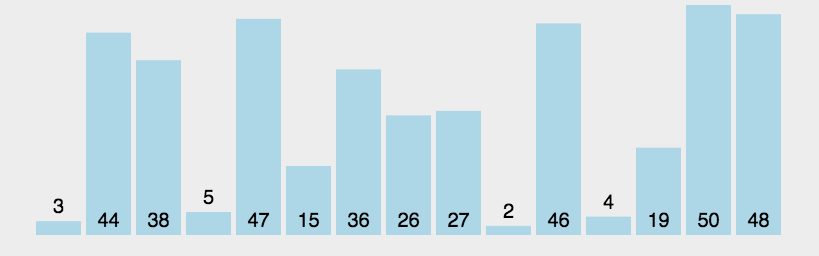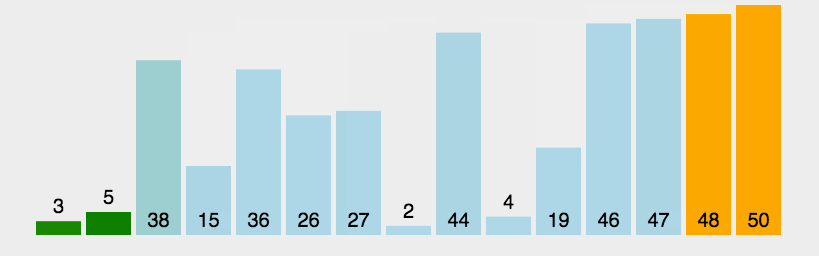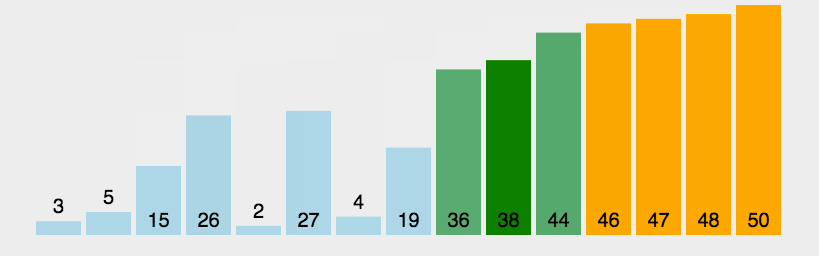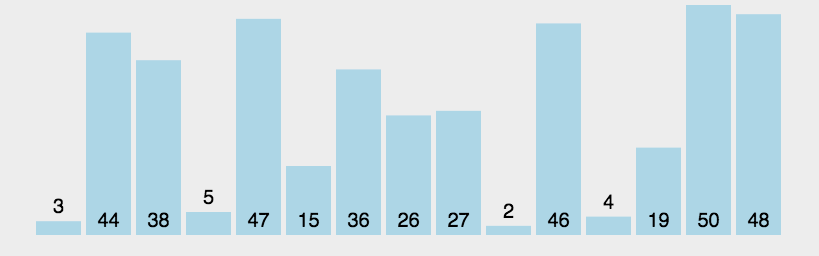本篇文章給大家帶來了關于python的相關知識,其中主要介紹了關于冒泡排序的相關問題,包括了算法描述、分析、代碼實現等等內容,下面一起來看一下,希望對大家有幫助。

推薦學習:python視頻教程
1. 算法描述
冒泡排序(Bubble Sort)是一種簡單的排序算法。它重復地遍歷要排序的數列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。遍歷數列的工作是重復地進行直到沒有再需要交換,也就是說該數列已經排序完成。這個算法的名字由來是因為越小的元素會經由交換慢慢“浮”到數列的頂端。
2. 算法分析
1. 比較相鄰的元素。如果第一個比第二個大(升序),就交換他們兩個。
2. 對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最后一對。這步做完后,最后的元素會是最大的數。
3. 針對所有的元素重復以上的步驟,除了最后一個。
4. 持續每次對越來越少的元素重復上面的步驟,直到沒有任何一對數字需要比較。
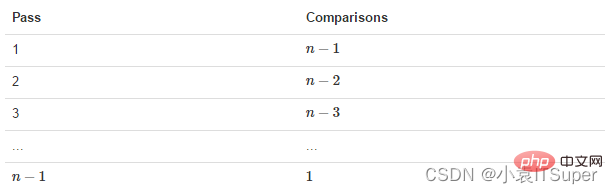
那么我們需要進行n-1次冒泡過程,每次對應的比較次數如下圖所示:
3. 動圖展示
看明白了運行流程,我們再來看看動圖實現:
4. 代碼實現
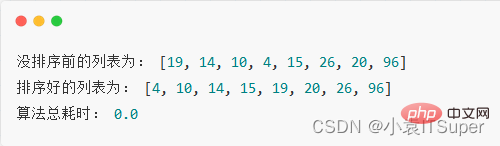
我們對如下無序列表進行排序
實現代碼:
import timepop_list = [19, 14, 10, 4, 15, 26, 20, 96]print("沒排序前的列表為:", pop_list)# 記錄開始時間start = time.time()# 外層循環控制輪數for i in range(len(pop_list) - 1): # 內層循環控制比較次數 for j in range(len(pop_list) - i - 1): # 如果前一個數字比后一個數字大,就交換位置 if pop_list[j] > pop_list[j + 1]: # python特有交換位置方式 pop_list[j], pop_list[j + 1] = pop_list[j + 1], pop_list[j]print("排序好的列表為:", pop_list)# 記錄結束時間end = time.time()print("算法總耗時:", end - start)
運行結果:
5. 算法升級
在循環中定義了一個變量count,如果第一次循環后count沒有變化,就說明輸入的是有序序列,這時我們直接return退出循環,這時候的時間復雜度為
O(n)
實現代碼:
import timedef bubble_sort(pop_list): for j in range(len(pop_list) - 1, 0, -1): count = 0 for i in range(0, j): if pop_list[i] > pop_list[i + 1]: pop_list[i], pop_list[i + 1] = pop_list[i + 1], pop_list[i] count += 1 if count == 0: returnpop_list = [19, 14, 10, 4, 15, 26, 20, 96]print("沒排序前的列表為:", pop_list)# 記錄開始時間start = time.time()bubble_sort(pop_list)print("排序好的列表為:", pop_list)# 記錄結束時間end = time.time()print("算法總耗時:", end - start)
運行結果:
6. 時間復雜度分析
- 最優時間復雜度:
O(n)(表示遍歷一次發現沒有任何可以交換的元素,排序結束。)- 最壞時間復雜度:
O(n^2)- 穩定性:穩定
- 排序分析:待排數組中一共有8個數,第一輪排序時進行了7次比較,第二輪排序時進行了6比較,依次類推,最后一輪進行了1次比較。
- 數組元素總數為N時,則一共需要的比較次數為:
(N-1)+ (N-2)+ (N-3)+ ...1=N*(N-1)/2- 算法約做了
N^2/2次比較。因為只有在前面的元素比后面的元素大時才交換數據,所以交換的次數少于比較的次數。如果數據是隨機的,大概有一半數據需要交換,則交換的次數為N^2/4(不過在最壞情況下,即初始數據逆序時,每次比較都需要交換)。- 交換和比較的操作次數都與 N^2 成正比,由于在大O表示法中,常數忽略不計,冒泡排序的時間復雜度為
O(N^2)。
推薦學習:python視頻教程
 站長資訊網
站長資訊網